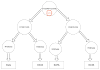
Trie is the most commonly used Ordered data structure in computer science. Trie is a Tree-based data structure that best suits efficient data storage and its retrieval. Each Node of Trie can link 26 other alphabetical keys with itself. This is also called Prefix tree or Digital Tree or Radix Tree. Trie data structure reduces the time complexity of searching string and pattern matching.
Types of Tries
There are commonly three types of Tries which are as follows:
- Compressed Trie
- Standard Trie
- Suffix Trie
Advantage of Trie data structure
- Trie is the fastest data structure for information retrieval and data storage.
- Trie supports searching, Insertion and deletion in the least time complexity.
- Trie lets you print all words in lexicographic order.
- Trie facilitates Prefix search or autocomplete features.
Disadvantage of Trie data structure
- They need lots of memory for storing characters.
- Time complexity increase for non-prefix words.
Basic Operation on Trie
- Insertion of new Node in Trie
- Deletion of a word in Trie
- Searching a word in Trie
Implementation of Trie
Implementation of Trie can be done by using arrays and storing references of the next substrings of that trie.
class node
{
public:
bool end;
node* next[26];
node(){
end=false;
for(int i=0;i<26;i++){
next[i]=NULL;
}
}
};
Let us see the code to Insert and search any Word in Trie. Strings will be stored from Top to button. we will use a Boolean variable to indicate the end of string inserted.
Insertion and searching in C++
#include<bits/stdc++.h>
using namespace std;
class Trie{
public:
class node
{
public:
bool end;
node* next[26];
node(){
end=false;
for(int i=0;i<26;i++){
next[i]=NULL;
}
}
};
node* trie;
Trie(){
trie= new node();
}
void insert(string word)
{
int i=0;
node* it=trie;
while(i<word.size())
{
if(it->next[word[i]-'a']==NULL)
it->next[word[i]-'a']= new node();
it=it->next[word[i]-'a'];
i++;
}
it->end=true;
}
bool search(string word)
{
int i=0;
node* it=trie;
while(i<word.size())
{
if(it->next[word[i]-'a']==NULL)
return NULL;
it=it->next[word[i]-'a'];
i++;
}
return it->end;
}
};
int main()
{
Trie* myTrie = new Trie();
vector<string> word = {"hii","akhil","dubey"};
for(auto w: word)
{
myTrie->insert(w);
}
if(myTrie->search("akhil"))
{
cout<<" akhil Found in The Trie"<<endl;
}
else{
cout<<"akhil does not found in this Trie"<<endl;
}
return 0;
}
Insertion and searching in Trie in Java
public class Trie {
class node{
boolean wordEnd;
node[] next = new node[26];
node()
{
wordEnd=false;
for(int i=0;i<26;i++)
{
next[i]=null;
}
}
}
node root;
Trie()
{
root= new node();
}
void insert(String s)
{
node it=root;
for(int i=0;i<s.length();i++)
{
if(it.next[s.charAt(i)-'a']==null)
{
it.next[s.charAt(i)-'a']= new node();
}
it=it.next[s.charAt(i)-'a'];
}
it.wordEnd=true;
}
boolean search(String s)
{
node it=root;
for(int i=0;i<s.length();i++)
{
if(it.next[s.charAt(i)-'a']==null)
{
return false;
}
it=it.next[s.charAt(i)-'a'];
}
return it.wordEnd;
}
public static void main(String[] args) {
// TODO Auto-generated method stub
System.out.println("hello Program ");
Trie t = new Trie();
t.insert("hello");
t.insert("akhils");
t.insert("dubey");
if(t.search("akhil"))
System.out.println("Akhil is Present ");
else
System.out.println("Not Present ");
}
}
Also Read - [ Median of two sorted Arrays ]
Time complexity for operations on Trie
Trie complexity to insert a word in Trie is O(n).
Space Complexity to insert a word in Trie is O(AxBxC). where A is number of words and B is total length of words and C is Size Of character.
Time Complexity to search a word in Trie is O(n).
Important questions on Trie data Structure
Practice these question to get better view on Trie data structure. this is favorite topic of tech interviews.
- Find Duplicate rows in a Binary Matrix
- Delete duplicate folder in a system using Trie
- CamelCase matching
- Implement magic dictionary
- Lexicographical numbers
- Top K frequent words
- Distinct echo substrings
- Maximum XOR of two numbers in a Array
These are some good level questions based on Trie data structure You can explore much more question on it
